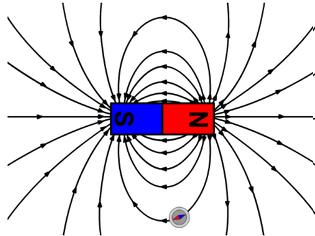
Για να παραστήσουμε ένα μαγνητικό πεδίο χρησιμοποιούμε τις (νοητές) μαγνητικές δυναμικές γραμμές, οι οποίες μας δείχνουν την μορφή του μαγνητικού πεδίου που εμφανίζεται γύρω από τους μαγνήτες ή τα ηλεκτρικά ρεύματα.
Ένα χρήσιμο μέγεθος στον ηλεκτρομαγνητισμό είναι η μαγνητική ροή Φ. Μας δείχνει «πόσο μαγνητικό πεδίο περνάει μέσα από μια επιφάνεια». Στο παραπάνω σχήμα η μαγνητική ροή εξαρτάται από την ένταση του μαγνητικού πεδίου B και το εμβαδόν της επιφάνειας S: Φ=Β•S. Mπορεί να πεί κανείς ότι εκφράζει τον αριθμό των δυναμικών γραμμών που διασχίζει την επιφάνεια. Όσο πιο πυκνές είναι οι γραμμές ή όσο πιο μεγάλη είναι η επιφάνεια S, τόσο μεγαλύτερη θα είναι η μαγνητική ροή Φ.
Ένα από τα εντυπωσιακότερα ηλεκτρομαγνητικά φαινόμενα προκαλείται εξαιτίας της μεταβολής της μαγνητικής ροής. Όταν η μαγνητική ροή που διασχίζει ένα κλειστό κύκλωμα μεταβάλλεται, τότε σύμφωνα με το νόμο της ηλεκτρομαγνητικής επαγωγής του Faraday, δημιουργείται ηλεκτρικό ρεύμα.
Το φαινόμενο αυτό γίνεται ακόμα πιο εντυπωσιακό αν πραγματοποιηθεί με έναν κυκλικό υπεραγωγό. Οι υπεραγωγοί έχουν την εντυπωσιακή ιδιότητα, όταν βρίσκονται κάτω από μια συγκεκριμένη χαμηλή θερμοκρασία, το ηλεκτρικό ρεύμα να ρέει στο εσωτερικό τους χωρίς καμμία αντίσταση! Έτσι, αν με κάποιο τρόπο μεταβάλλουμε στιγμιαία την μαγνητική ροή που διασχίζει κάποιον υπεραγώγιμο δακτύλιο, τότε σύμφωνα με το νόμο του Faraday δημιουργείται ένα κυκλικό ηλεκτρικό ρεύμα.
Το μαγνητικό πεδίο που δημιουργεί ένας ρευματοφόρος κυκλικός αγωγός
Επειδή στον υπεραγωγό δεν υπάρχει ωμική αντίσταση, το ρεύμα αυτό παραμένει επ’ άπειρον. Και δημιουργεί ένα μόνιμο μαγνητικό πεδίο γύρω από τον δακτύλιο. Θα περίμενε κανείς ότι η μαγνητική ροή που διασχίζει την επιφάνεια του κυκλικού υπεραγωγού να μπορεί να πάρει μια οποιαδήποτε τιμή. Δηλαδή, να μεταβάλλεται με συνεχή τρόπο. Κι όμως. Αποδεικνύεται ότι το ηλεκτρικό ρεύμα στον υπεραγωγό ρυθμίζεται «αυτόματα» έτσι ώστε η μαγνητική ροή στον δακτύλιο να παίρνει τιμές που είναι ακέραια πολλαπλάσια ενός κβάντου μαγνητικής ροής: . Δηλαδή η μαγνητική ροή είναι κβαντωμένη.
Στις αρχές της δεκαετίας του 1950 οι Fritz London και L. Onsager προέβλεψαν θεωρητικά το φαινόμενο της κβάντωσης της μαγνητικής ροής.(1), (2) Και στις αρχές της δεκαετίας του 1960 οι φυσικοί πειραματιζόμενοι με υπεραγώγιμους κυκλικούς αγωγούς διαπίστωσαν ότι πράγματι, η μαγνητική ροή που διέσχιζε το επίπεδο κυκλικών αγωγών δεν μεταβαλλόταν με συνεχή τρόπο αλλά κβαντισμένα(3),(4).
Kανονικά, η κβάντωση δεν μπορεί να παρατηρηθεί σε ένα μακροσκοπικό σύστημα. Οι υπεραγωγοί όμως είναι ένα σπάνιο είδος υλικών στα οποία οι κβαντομηχανικές παραξενιές εκδηλώνονται σε μακροσκοπική κλίμακα. Στους υπεραγωγούς αποδεικνύεται θεωρητικά και επιβεβαιώνεται πειραματικά, ότι η μαγνητική ροή μπορεί να πάρει τιμές που είναι ακέραια πολλαπλάσια μιας πεπερασμένης στοιχειώδους μαγνητικής ροής. Είναι αξιοσημείωτο ότι το κβάντο της μαγνητικής ροής εξαρτάται μόνο από δύο σταθερές: το ηλεκτρικό φορτίο του ηλεκτρονίου και την σταθερά Planck.
Μια ημικλασική αλλά … ημιπαράνομη προσέγγιση
Η μαγνητική ροή που διασχίζει έναν υπεραγώγιμο κυκλικό αγωγό εξαρτάται από το ηλεκτρικό ρεύμα που τον διαρρέει, το οποίο με τη σειρά του εξαρτάται από την κυκλική κίνηση των ηλεκτρονίων. Για να προκύψει η κβάντωση της μαγνητικής ροής, υποθέτουμε ότι τα ηλεκτρόνια πρέπει να βρίσκονται σε διακριτές ενεργειακές στάθμες όπως στο άτομο του υδρογόνου(5). Σύμφωνα με την αρχή του Bohr, ένα ηλεκτρόνιο που κινείται σε κυκλική τροχιά ακτίνας r πρέπει να ικανοποιεί την σχέση: όπου n=1, 2, 3 Στην περίπτωση του υπεραγώγιμου βρόχου μπορούμε να θεωρήσουμε ότι τα ηλεκτρόνια κινούνται σε κυκλική τροχιά μέσα σε ένα ομογενές μαγνητικό πεδίο B εξαιτίας της δύναμης Lorentz που παίζει τον ρόλο της κεντρομόλου επιτάχυνσης: . Από τις εξισώσεις (1) και (2) προκύπτει ότι: , δηλαδή η μαγνητική ροή είναι κβαντωμένη.
Ο παραπάνω συλλογισμός μας οδηγεί μεν στο σωστό αποτέλεσμα, αλλά εμπεριέχει «ακροβασίες», π.χ. το μαγνητικό πεδίο δεν είναι ομογενές ή στον κυκλικό υπεραγωγό δεν υπάρχουν μεμονωμένα ηλεκτρόνια που κινούνται σε καθορισμένες τροχιές Bohr. Η περιγραφή του φαινομένου πρέπει να γίνει κβαντομηχανικά. Χρησιμοποιώντας την μακροσκοπική κυματοσυνάρτηση των ζευγών ηλεκτρονίων Cooper (εξού και ο παράγοντας 2 στο κβάντο ροής), η κβάντωση της μαγνητικής ροής προκύπτει από την απαίτηση μονοτιμίας της κυματοσυνάρτησης που επιβάλλει η συνολική μεταβολή της φάσης της κατά μήκος του κυκλικού αγωγού να είναι ακέραιο πολλαπλάσιο του 2π. Μπορεί ο κβαντομηχανικός υπολογισμός του κβάντου μαγνητικής ροής να φαίνεται μαθηματικά «συμπυκνωμένος», στην πραγματικότητα όμως είναι πολύ απλός (περισσότερες λεπτομέρειες εδώ: Τhe Feynman Lectures on Physics Vol. III, 21–7 Flux quantization).
Το κβάντο μαγνητικής ροής είτε υπολογιστεί ημικλασικά είτε κβαντομηχανικά προκύπτει εξίσου πολύ μικρό. Για να το αισθανθούμε: η μαγνητική ροή του – εν γένει ασθενούς – μαγνητικού πεδίου της Γης που διασχίζει επιφάνεια 1 mm2 είναι περίπου 0.5×10−10 Weber, δηλαδή αποτελείται από 25.000 κβάντα μαγνητικής ροής.
Βιβλιογραφία:
1. Fritz London, Superfluids, Volume I: Macroscopic Theory of Superconductivity (Wiley, New York, 1950),
2. L. Onsager (1952), «Interpretation of the de Haas–van Alphen effect «, Philosophical Magazine 43, 1006–1008 [όλες οι λεπτομέρειες περιέχονται εδώ: Magnetic Flux Through a Superconducting Ring]
3. Bascom S. Deaver, Jr. και William M. Fairbank: «Experimental Evidence for Quantized Flux in Superconducting Cylinders»
4. R. Doll και M. Näbauer: «Experimental Proof of Magnetic Flux Quantization in a Superconducting Ring».
5. «Μαγνητικό μονοπώλιο», περιοδικό QUANTUM, Ιούλιος/Αύγουστος 1995
https://physicsgg.me/
tinanantsou.blogspot.gr











